Linear Regression
Logistic Regression
Different from previous linear regression, logistic regression output discreate value like 0 or 1. So logistic regression is a claasification algorithm.
Indeed, logistic regreesion is a linear regression, we wrap a step function (sigmoid function) on linear regression making the output to be discreate.
The sigmoid function $g(z)$ looks like below:
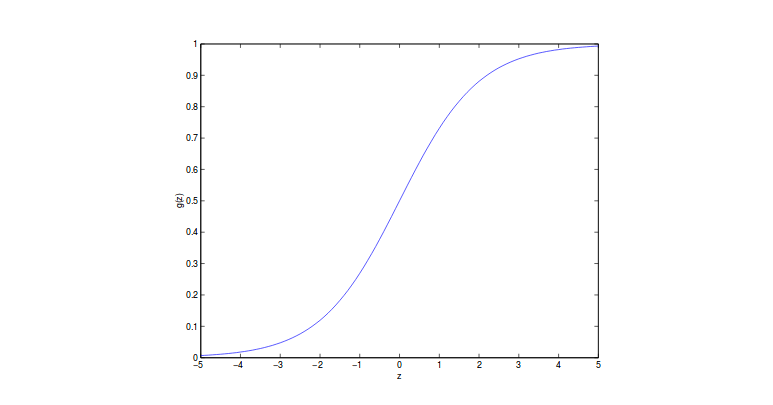
Then the output will be in the range 0 and 1. And if the function ouput is larger than or equal to 0.5, we will say it’s positive class as y = 1, vice versa.
\[h_\theta(x) = g(\theta^Tx) = \frac{1}{1+exp(-\theta^Tx)}\]What’s more, we will take the output as a probability $p(y=1|x,\theta)$.
Why sigmoid function has such property? And why don’t we choose other function that can map output to range 0 to 1?
That’s because binary classfication is Bernolli Distribution which is in exponential family! Suppose $p$ is the parameter for Binomial Distribution.
\[f(x|p) = p^x*(1-p)^{1-x} = exp[In(p^x*(1-p)^{1-x})]\\ = exp[xIn(p) + (1-x)In(1-p)]\\ = exp[x(In(p)-In(1-p))+In(1-p)]\\ = exp[xIn(\frac{p}{1-p})+In(1-p)]\]So right now, the pdf of Bernolli Distribution is expressed in the form of exponential family. Below are the parameters in exponential family.
\[T(x) = x\\ \eta = In(\frac{p}{1-p})\\ a(\eta) = In(1-p)\\ b(y) = 1\]$\eta$ is nature parameter, when $a$,$b$ and $T$ is fixed, changing $\eta$ can get a new distribution.
\[p = \frac{1}{1+e^{-\eta}}\]This is exactly sigmoid function! That’s the reason why the output is a probability (p is the probability x=1 in Bernolli Distribution)!
Cost function
In this section, that’s talk about the cost function for logistic regression. In the basic machine learning class, the lecturer will just tell you the cost function looks like below:
\[J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y_i\log h_\theta(x_i)+(1-y_i)\log(1-h_\theta(x_i))]\]But why? - Maximum likelyhood Estimation!
As we discuss before, $h_\theta(x) = p(y=1|x)$. Suppose each dots are i.i.d.
\[L(\theta) = \sum_{i=1}^m[p(y_i=1|x_i)^{y_i}p(y_i=0|x_i)^{1-y_i}]\]Take the log on likelihood function. Denote $p(y=1|x) = p(x)$.
\[\log L(\theta) = \sum [y_i\log p(x) + (1-y_i)(1-p)]\]Since $p = h_\theta(x)$ and add a negative signal in front of equation we can derive our cost function!
Once we get the cost funciton, we can minimize it and get optimal $\theta$. Because this is a convex function (free of local minimum), we can use gradient descent.
\[h_\theta(x) = g(\theta^Tx) = \frac{1}{1+exp(-\theta^Tx)}\]Referenecs
机器学习总结之逻辑回归Logistic Regression 指数分布族(The Exponential Family)与广义线性回归(Generalized Linear Model GLM) 从指数分布族去推导出广义线性模型