Neural NetWork
Perceptrons Neuron
Perceptrons were developed in the 1950s and 1960s by Frank Rosenblatt which were earliest types of neural network. A perceptrons takes several binary inputs (0 or 1) and outputs a single binary output.
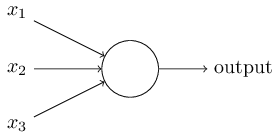
In the example the perceptron has three inputs $x_1$, $x_2$ and $x_3$ and there are weights $w_1$, $w_2$ and $w_3$ for each input. If the weighted sum $\sum w_jx_j$ are higher than a threshold value, the perceptron will output 1, vice versa.
\[output=\left\{ \begin{array}{rcl} 1 & & {\sum w_jx_j > threshold}\\ 0 & & {\sum w_jx_j \leq threshold}\\ \end{array} \right.\]Set bias $b = -threshold$, above expression can be simplified as:
\[output=\left\{ \begin{array}{rcl} 1 & & {\sum w_jx_j + b> 0}\\ 0 & & {\sum w_jx_j +b \leq 0}\\ \end{array} \right.\]Using several perceptrons, we can build a simple neural network.
Sigmoid Neuron
For perceptrons neuron, there is a significan drawbacks. The output changes suddenly, so small changes in weights or bias won’t change the output. It would be very difficult to calibrate weigts and bias.

To address this issue, we can apply so called activation function. If we use sigmoid function as activation function, then the neuron is called sigmoid neuron. sigmoid function has expression below:
\[\sigma(z) = \frac{1}{1+e^{-z}}\] \[z = \sum w_jx_j + b\]And its shape was like below:

After applying this activation function, any small changes in weights or bias will result in small change in output which is a good property we desired.
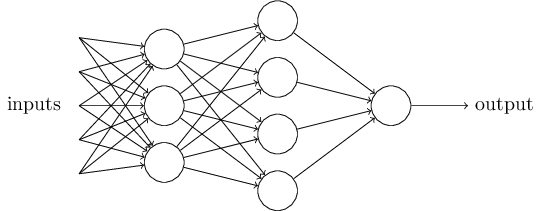
If there is network which is made up by multiple layer of sigmold neurons, such network would be called multilayer perceptrons or MLPs despite it’s not made up by perceptrons.