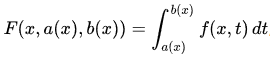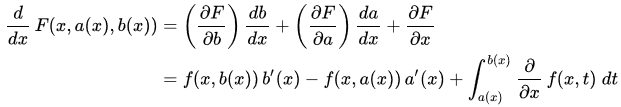Motivation for Local Volatility
In the market, implied volatility can be back out by using obeservable market quotes. Options with different strikes and expirations have different Black-Scholes implied volatility. So traders have to continuously change the volatility assumption of BS formula to match the market quotes.
To avoid this tedious work, naturally, traders want loose the constant volatility assumption and build a volatility model so that the model can always generate no-arbitrage option price.
Fokker Planck Equation
Assumption
Fokker Planck Equation is a PDE that the probability density function (pdf) of future underlying asset price should satisfy.
Suppose the underlying asset follows below SDE in risk-neutral space:
\[dS_t = \mu(S,t)dt + \sigma(S,t)dw_t\]Suppose there is an arbitrary twice differenciable function $f$. In finance, $f(S_t)$ can be considered as payoff function.
Expectation Euqation
Applying Ito’s Lemma to the $f(S_t)$:
\[df = \frac{\partial f}{\partial s}dS + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}dSdS\\ = (\frac{\partial f}{\partial s}\mu + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2)dt + \frac{\partial f}{\partial s}\sigma dw\]Take expectation on both side, then random term $dw$ will vanish:
\[E[df] = E[(\frac{\partial f}{\partial s}\mu + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2)dt]\]Rearrange the formula:
\[\frac{dE(f)}{dt} = E[\frac{\partial f}{\partial s}\mu + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2]\]Next step will be calculate the $E(f(S_t))$. And we defined a pdf function $p(S,t)$ which can be intuitively considered as the probability of underlying asset end up with S at time t. t can be viewed as maturity time. So it’s fixed. The two expectations can be expressed as below:
\[E[f(S_t)] = \int_{-\infty}^{+\infty} f(s)p(s,t)ds\]And
\[E[\frac{\partial f}{\partial s}\mu + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2] = \int_{-\infty}^{+\infty} (\frac{\partial f}{\partial s}\mu + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2)p(s,t)ds\\ =\int_{-\infty}^{+\infty} \frac{\partial f}{\partial s}\mu p(s,t)ds + \int_{-\infty}^{+\infty}\frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2p(s,t)ds\]Calculate the derivative on First Expectation - Left Hand Side
\[\frac{dE(f)}{dt} = \frac{d(\int_{-\infty}^{+\infty} f(s)p(s,t)ds)}{dt}\]Just applying the Leibniz’s Rule
So the result of the Left Hand Side is:
\[\frac{dE(f)}{dt} = \int_{-\infty}^{+\infty} \frac{\partial}{\partial t}[f(s)p(s,t)]ds \\ = \int_{-\infty}^{+\infty} f(s)\frac{\partial p(s,t)}{\partial t}ds\]Calculate Second Expectation - Right Hand Side
Denote $\frac{\partial f}{\partial s}$ as $f’(s)$ and $\frac{\partial^2 f}{\partial s^2}$ as $f’‘(s)$. Let’s calculate the first intergral.
\[\int_{-\infty}^{+\infty} f'(s)\mu(s,t) p(s,t)ds = f(s)\mu(s,t) p(s,t)|^{\infty}_{-\infty} - \int_{-\infty}^{+\infty} f(s)\frac{\partial [\mu(s,t) p(s,t)]}{\partial s}ds \\ = - \int_{-\infty}^{+\infty} f(s)\frac{\partial [\mu(s,t) p(s,t)]}{\partial s}ds\]The intergration by part is used here, where
\[u = f(x), v = \mu(s,t) p(s,t)\]
And, the probability of asset price goes into infinity is 0 almost surely
\[\lim_{s \to \infty} p(s,t) = 0\]
so $uv$ term disappear in the last euqation
Then the second intergral is calculated below:
\[\frac{1}{2}*\int_{-\infty}^{+\infty}f''(s)\sigma^2(s,t)p(s,t)ds \\ =\frac{1}{2}*f'(s)\sigma^2(s,t) p(s,t)|^{\infty}_{-\infty} - \frac{1}{2}*\int_{-\infty}^{+\infty} f''(s)\frac{\partial [\sigma^2(s,t) p(s,t)]}{\partial s}ds \\ = - \frac{1}{2}*\int_{-\infty}^{+\infty} f'(s)\frac{\partial [\sigma^2(s,t) p(s,t)]}{\partial s}ds \\ = - \frac{1}{2}*[(f(s)\frac{\partial [\sigma^2(s,t) p(s,t)]}{\partial s})|^{\infty}_{-\infty} - \int_{-\infty}^{+\infty} f(s)\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2}ds] \\ = \frac{1}{2}*\int_{-\infty}^{+\infty} f(s)\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2}ds\]The intergration by part is used twice here, the first time
\[u = f'(x), v = \sigma^2(s,t) p(s,t)\]
the second time
\[u = f(x), v = \frac{\partial [\sigma^2(s,t) p(s,t)]}{\partial s}\]
And, the probability of asset price goes into infinity is 0 almost surely
\[\lim_{s \to \infty} p(s,t) = 0\]
so $uv$ term disappear
Don’t get lost here! Just substitude the two intergral results back to original formula:
\[E[\frac{\partial f}{\partial s}\mu + \frac{1}{2}*\frac{\partial^2 f}{\partial s^2}\sigma^2] = \frac{1}{2}*\int_{-\infty}^{+\infty} f(s)\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2}ds - \int_{-\infty}^{+\infty} f(s)\frac{\partial [\mu(s,t) p(s,t)]}{\partial s}ds \\ = \int_{-\infty}^{+\infty}f(s)[\frac{1}{2}*\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2} - \frac{\partial [\mu(s,t) p(s,t)]}{\partial s}]ds\]Above is the final result for second expectation.
Left Hand Side = Right Hand Side
\[\int_{-\infty}^{+\infty} f(s)\frac{\partial p(s,t)}{\partial t}ds = \int_{-\infty}^{+\infty}f(s)[\frac{1}{2}*\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2} - \frac{\partial [\mu(s,t) p(s,t)]}{\partial s}]ds\]Rearrange the euqation:
\[\int_{-\infty}^{+\infty} f(s)[\frac{\partial p(s,t)}{\partial t} - \frac{1}{2}*\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2} + \frac{\partial [\mu(s,t) p(s,t)]}{\partial s}]ds = 0\]This intergral is satisfied with any payoff function $f(s)$. As a result:
\[\frac{\partial p(s,t)}{\partial t} - \frac{1}{2}*\frac{\partial^2 [\sigma^2(s,t) p(s,t)]}{\partial s^2} + \frac{\partial [\mu(s,t) p(s,t)]}{\partial s} = 0\]Finally! This the the Fokker Planck Equation which should be satisfied by pdf of underlying asset price.
Fokker Planck Equation and Local Volatility
Why we spend so much time on deriving Fokker Planck Equation? Because in next article, this equation will be the basis to derive the formula of $\sigma^2(s,t)$ which is the what we want at the beginning.
References
Fokker Planck Equation Derivation: Local Volatility, Ornstein Uhlenbeck, and Geometric Brownian
The Dupire Formula
Derivation of Local Volatility
DerivationofFokker–Planck EquationfortheLocal VolatilityModel